N Notes

Appearance

十种排序算法

2018-10-24-view(s)-comment(s)- min read

前言 ​

  • 从无聊的排序算法开始: n 是待排数的个数，a[n] 是待排序序列，其它变量字面意思。
  • 之所以示意图是手绘版，是因为抽不到炼狱茨木童子。

I - 冒泡排序 ​

简单来说 ​

冒泡的一轮

Show Me The Code ​

python
def bubble_sort(a: list[float], n: int) -> list[float]:
    for i in range(n-1):
        not_swap = True
        for j in range(1, n-i):
            if a[j] < a[j-1]:
                a[j], a[j-1] = a[j-1], a[j]
                not_swap = False
        if not_swap:
            break
    return a

分析 ​

  • 是稳定排序。
  • 平均时间复杂度：O(n2)。

II - 快速排序 ​

简单来说 ​

快排的一轮

Show Me The Code ​

python
def quick_sort(a: list[float], n: int) -> list[float]:
    l, r, r_to_l = 0, n-1, True
    while l < r:
        if a[l] > a[r]:
            a[l], a[r] = a[r], a[l]
            r_to_l = not r_to_l

        if r_to_l:
            r -= 1
        else:
            l += 1

    if l >= 2:
        quick_sort(a[:l], l)

    if n-1-l >= 2:
        quick_sort(a[l+1:], n-1-l)

    return a

分析 ​

  • 是不稳定排序。
  • 平均时间复杂度：O(nlog2n)。

III - 插入排序 ​

简单来说 ​

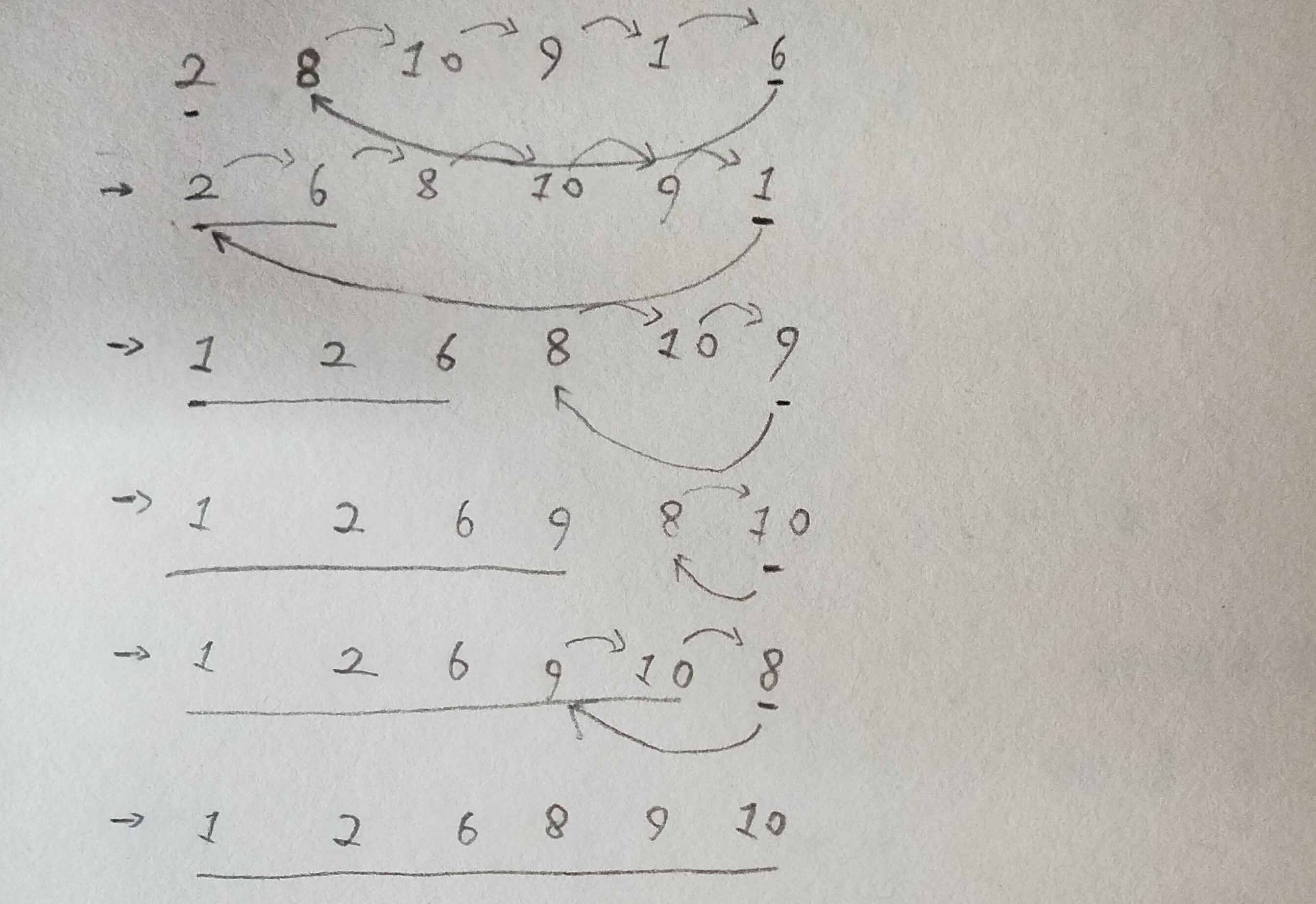
插入排序的若干轮

Show Me The Code ​

python
def insert_sort(a: list[float], n: int) -> list[float]:
    for i in range(1, n):
        for j in range(i):
            if a[n-1] < a[j]:
                a = [*a[:j], a[n-1], *a[j:n-1]]
                break
            elif j == i-1:
                a = [*a[:j+1], a[n-1], *a[j+1:n-1]]
    return a

分析 ​

  • 是稳定排序。
  • 平均时间复杂度：O(n2)。

IV - 希尔排序 ​

简单来说 ​

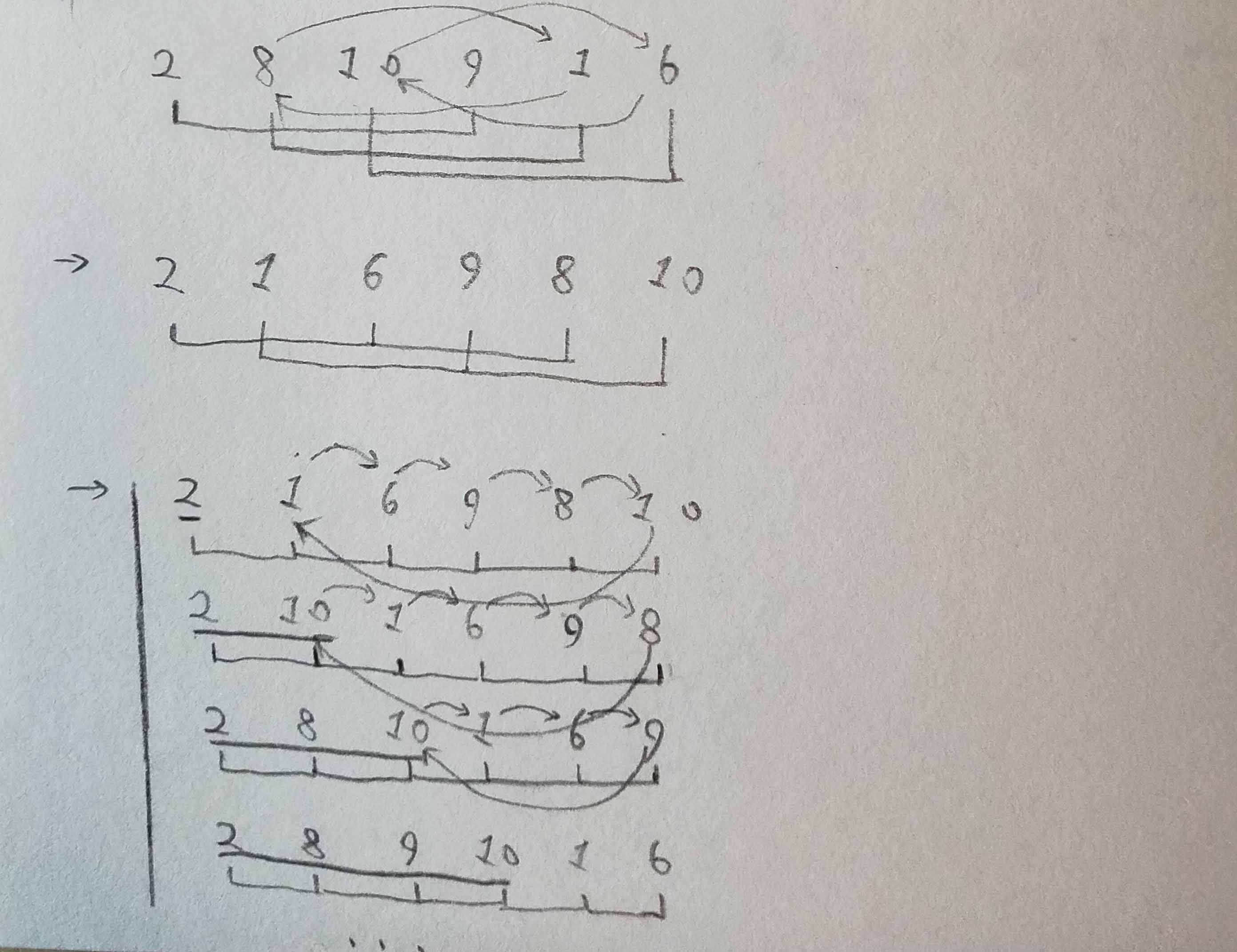
希尔排序的若干轮

Show Me The Code ​

python
def Shell_Sort(a,n):
    step = n/2
    while step:
        # 分组
        groups = []
        indexFirst = 0
        while not indexFirst==step:
            groups.append(a[indexFirst::step])
            indexFirst += 1
        # 对各组直接插入排序
        for i in range(len(groups)):
            Insert_Sort(groups[i],len(groups[i]))
        # 合并分组
        indexFirst = 0
        while not indexFirst==step:
            a[indexFirst::step] = groups[indexFirst]
            indexFirst += 1
        # 缩减增量，新一轮
        step /= 2

分析 ​

  • 是不稳定排序。
  • 平均时间复杂度：O(n1.3)。

V - 选择排序 ​

简单来说 ​

选择排序的若干轮

Show Me The Code ​

python
def Select_Sort(a,n):
    for i in range(n-1):
        indexMin = i
        for j in range(i+1,n):
            if a[j]<a[indexMin]:
                indexMin = j
        if not indexMin==i:
            a[i],a[indexMin] = a[indexMin],a[i]

分析 ​

  • 是不稳定排序。
  • 平均时间复杂度：O(n2)。

VI - 堆排序 ​

简单来说 ​

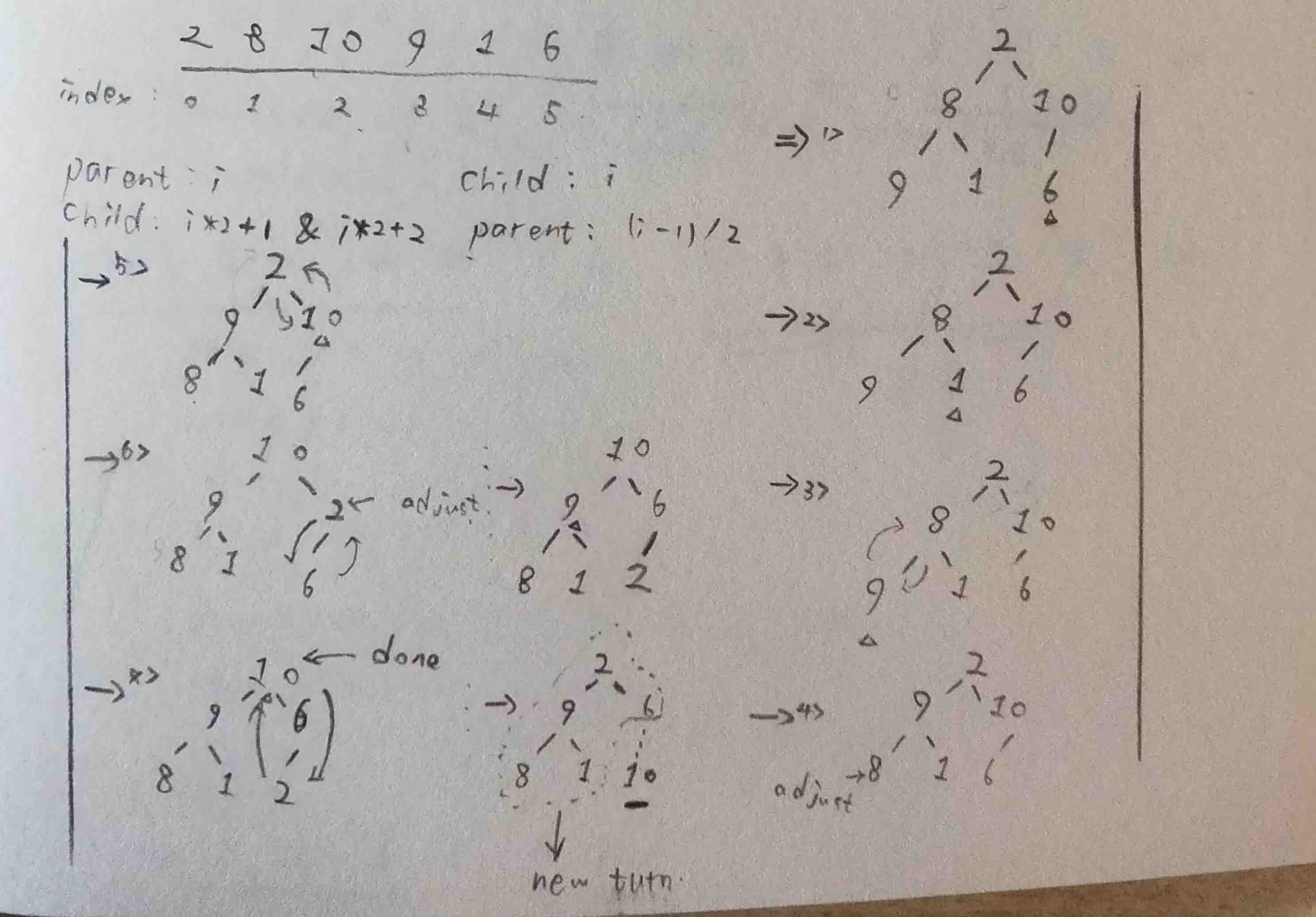
堆排序的一轮

Show Me The Code ​

python
# 调整二叉树结构以构建大顶堆
def Adjust_Heap(a,indexSwapped,indexFinal):
    if indexSwapped*2+1<=indexFinal:# 有至少一个子节点
        top,left = indexSwapped,indexSwapped*2+1
        right = indexSwapped*2+2 if not indexSwapped*2+2>indexFinal else indexSwapped*2+1
        if a[right]-a[top]>a[left]-a[top] and a[right]>a[top]:
            a[top],a[right] = a[right],a[top]
            Adjust_Heap(a,right,indexFinal)
        elif a[right]-a[top]<=a[left]-a[top] and a[left]>a[top]:
            a[top],a[left] = a[left],a[top]
            Adjust_Heap(a,left,indexFinal)

# 构建大顶堆
def Build_Heap(a,indexUntil,isFirst):
    if isFirst:
        for i in range(indexUntil,0,-1):
            if a[i]>a[(i-1)/2]:
                a[i],a[(i-1)/2] = a[(i-1)/2],a[i]
                Adjust_Heap(a,i,indexUntil)
    else:
        Adjust_Heap(a,0,indexUntil)

def Heap_Sort(a,n):
    Build_Heap(a,n-1,True)
    a[0],a[n-1] = a[n-1],a[0]
    for i in range(n-2,0,-1):
        Build_Heap(a,i,False)
        a[0],a[i] = a[i],a[0]

分析 ​

  • 是不稳定排序。
  • 平均时间复杂度：O(nlog2n)。

VII - 合并排序 ​

简单来说 ​

合并排序的若干轮

Show Me The Code ​

python
def Merge_Sort(a,beginIndex,endIndex):
    if endIndex-beginIndex<=1:
        if endIndex-beginIndex==1:
            (a[beginIndex],a[endIndex]) = (a[beginIndex],a[endIndex]) if a[beginIndex]<a[endIndex] else (a[endIndex],a[beginIndex])
    else:
        Merge_Sort(a,beginIndex,beginIndex+(endIndex-beginIndex)/2)
        Merge_Sort(a,beginIndex+(endIndex-beginIndex)/2+1,endIndex)
        partLeft = a[beginIndex:beginIndex+(endIndex-beginIndex)/2+1]
        partRight = a[beginIndex+(endIndex-beginIndex)/2+1:endIndex+1]
        tmp = []
        i,j = 0,0
        while i<beginIndex+(endIndex-beginIndex)/2-beginIndex+1 and j<endIndex-beginIndex-(endIndex-beginIndex)/2:
            if partLeft[i]>=partRight[j]:
                tmp.append(partRight[j])
                j += 1
            else:
                tmp.append(partLeft[i])
                i += 1
        if j<endIndex-beginIndex-(endIndex-beginIndex)/2:
            tmp += partRight[j:]
        if i<beginIndex+(endIndex-beginIndex)/2-beginIndex+1:
            tmp += partLeft[i:]
        a[beginIndex:endIndex+1] = tmp[:]

分析 ​

  • 是稳定排序。
  • 平均时间复杂度：O(nlog2n)。

VIII - 计数排序 ​

简单来说 ​

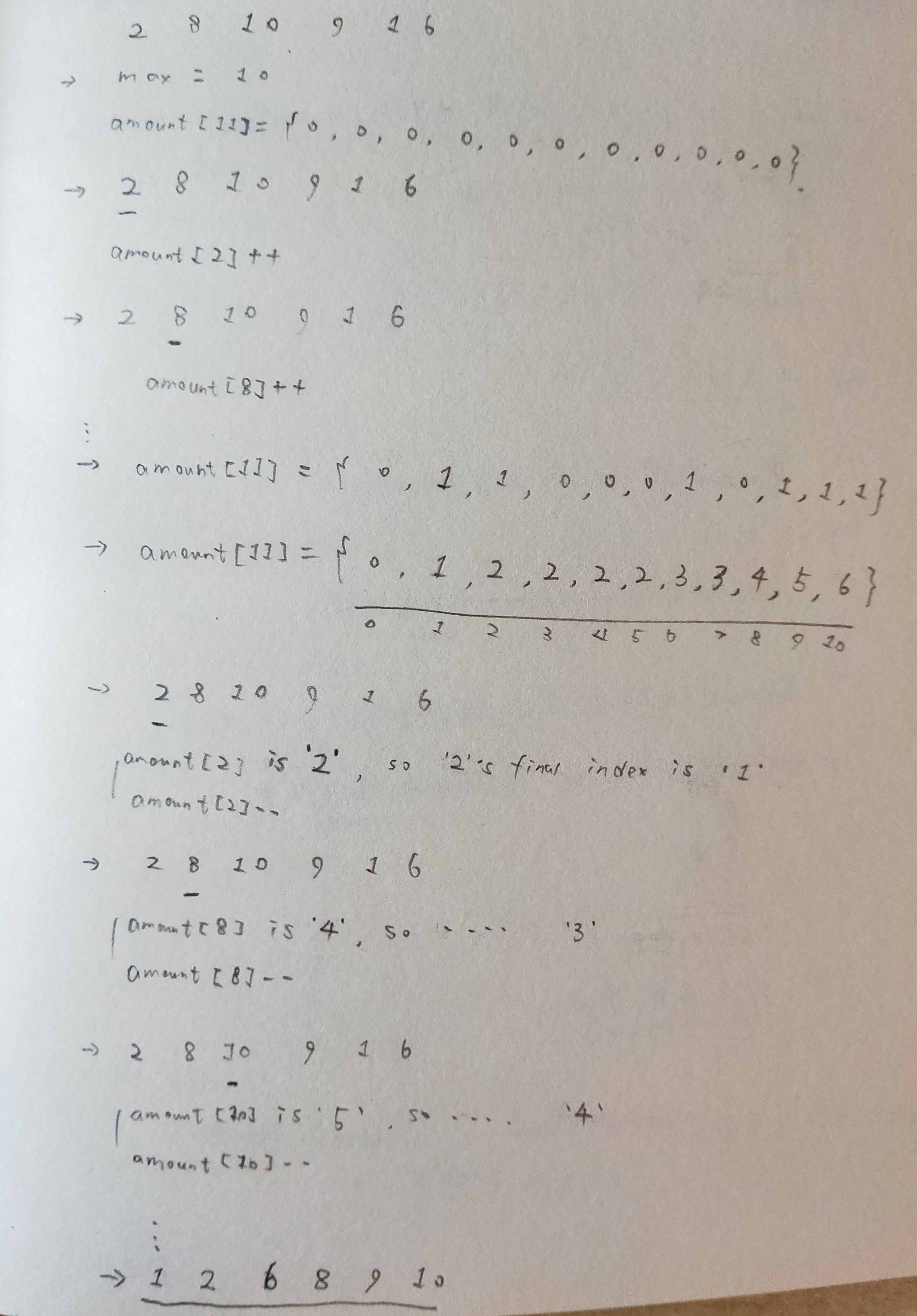
计数排序的若干轮

Show Me The Code ​

python
def Count_Sort(a,n):
    # 找出最大值
    max = a[0]
    for i in range(1,n):
        if a[i]>max:
            max = a[i]
    # 设定指定大小
    container = [0 for i in range(max+1)]
    # 计数
    for i in a:
        container[i] += 1
    for i in range(1,max+1):
        container[i] += container[i-1]
    # 排序
    tmp = [0 for i in range(n)]
    for i in a:
        tmp[container[i]-1] = i
        container[i] -= 1
    a[:] = tmp[:]

分析 ​

  • 是稳定排序。
  • 平均时间复杂度（k 与待排序数的范围相关）：O(n+k)。

IX - 桶排序 ​

简单来说 ​

桶排序的若干轮

Show Me The Code ​

python
def Bucket_Sort(a,n):
    max = a[0]
    for i in range(1,n):
        if a[i]>max:
            max = a[i]
    min = a[0]
    for i in range(1,n):
        if a[i]<min:
            min = a[i]

    gap = (max-min)/n+1

    amtBucket = (max-min)/gap+1

    groups = [[] for i in range(amtBucket)]
    for i in a:
        groups[(i-min)/gap].append(i)
    tmp = []
    for i in range(amtBucket):
        Quick_Sort(groups[i],0,len(groups[i])-1)
        tmp += groups[i] if not groups[i]==[] else []
        forShow = []
        for j in groups:
            for k in j:
                forShow.append(k)
    a[:] = tmp[:]

分析 ​

  • 是稳定排序。
  • 平均时间复杂度（k 与每个桶内数的个数相关）：O(n+k)。

X - 基数排序 ​

简单来说 ​

基数排序的若干轮

Show Me The Code ​

python
def Radix_Sort(a,n):
    groups,digit,amt = [[] for i in range(10)],1,0
    while amt<n:
        for i in a:
            groups[(i/digit)%10].append(i)
        tmp = []
        for i in range(10):
            tmp += groups[i]
        a[:] = tmp[:]
        Show_ThisMoment(a,1000,64,100)
        amt = len(groups[0])
        groups[:] = [[] for i in range(10)]
        digit *= 10

分析 ​

  • 是稳定排序。
  • 平均时间复杂度（k 与待排数的最高位数相关）：O(nk)。

排序算法总动员 ​

这是一个可爱的传送门

后语 ​

这拨儿排序，花太多时间了（终于结束了）。但也没什么好绝望的，我们此刻费尽心机想逃离的一切，有一天都会在记忆里成为一座开满黄水仙与蔷薇的花园。我们再也回不去了。

©陶清秋「蔷薇与黄水仙」「蔷薇与黄水仙」©Qingqiu